机器学习实践

训练流程

问题定义

  • 确定目标：明确问题的具体需求，例如是分类、回归、聚类、预测还是生成任务。

目标：获取高质量的数据，并将其转换为适合模型训练的格式。

数据收集与预处理

  • 数据收集：
    • 确定数据来源（公开数据集、企业内部数据、爬虫等）。
    • 收集足够的数据以支持模型训练。
  • 数据清洗：
    • 去除噪声、重复数据和异常值。
    • 填补缺失值。
  • 数据标注（对于有监督学习）：
    • 对数据进行标注，例如分类标签、边界框等。

模型的选择与训练

  • 选择算法：
    • 根据问题类型选择合适的算法，例如CNN用于图像分类，LSTM用于时间序列预测。
  • 模型架构设计：
    • 设计模型的结构，例如层数、神经元数量、激活函数等。

模型评估与优化

  • 对模型进行深入评估，并优化模型以达到最佳性能。

环境介绍

Anaconda：是一个流行的开源数据科学平台，主要用于 Python 和 R 编程语言的管理和开发。

  • 环境管理
    • Anaconda 允许用户创建、管理和切换不同的 Python 或 R 环境。每个环境可以安装不同的包版本，避免包冲突。例如，用户可以在一个环境中安装 Python 3.8 用于数据分析，而在另一个环境中安装 Python 3.10 用于机器学习项目。
  • 包管理
    • 它自带了包管理器 Conda，可以方便地安装、更新和卸载各种数据科学相关的包。比如，通过简单的命令 conda install numpy，就可以安装 NumPy 包，而无需担心依赖问题。

Anaconda 的核心价值在于巧妙地将不同项目环境相互隔离，有效避免因环境冲突而导致的运行错误，为开发流程带来极致的清晰与稳定，让开发者能够专注于代码逻辑，无需再为复杂的环境问题而烦恼。

环境准备

本实验需要下载Anaconda，并且配置Jupyter Notebook以及安装matplotlib、pandas、sklearn、numpy等包。

NumPy (Numerical Python)

  • 功能: NumPy是Python中用于科学计算的核心库。它提供了强大的N维数组对象（ndarray），以及用于处理这些数组的各种高效函数。

Pandas (Python Data Analysis Library)

  • 功能: Pandas是一个强大而灵活的数据分析和数据处理库。它构建在NumPy之上，提供了两种主要的数据结构：Series（一维带标签数组）和DataFrame（二维带标签表格数据）。

Matplotlib

  • 功能: Matplotlib是一个用于创建静态、动态、交互式可视化的Python库。它提供了一套完整的2D绘图功能，也可以扩展到3D绘图。

Scikit-learn (Sklearn)

  • 功能: Scikit-learn是一个免费的机器学习库，提供了各种分类、回归、聚类、降维以及模型选择和预处理工具。

  • 安装Anaconda

进入官网：Download Now | Anaconda 进行下载，如何下载和配置不多做赘述，网上大把教程。

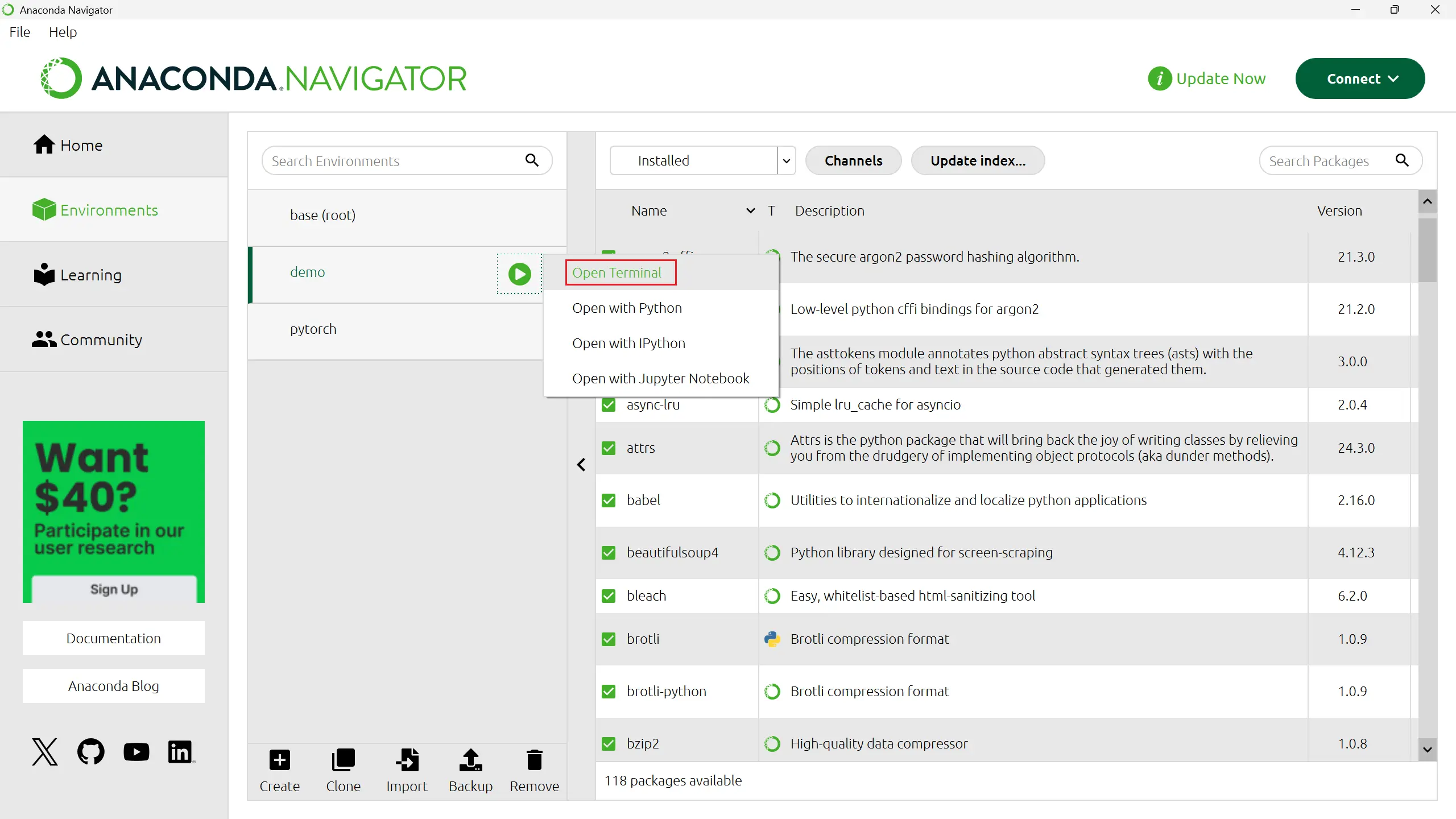
  • 在安装好Anaconda后，创建一个新的环境。名字随便起，选择python最新的版本就好。

image

点击绿色三角，点击“Open Terminal”。这会进入我们anaconda内置的命令行工具，我们要借助他来安装我们的包。

image

在命令行工具中依次输入：

1
conda install numpy
1
conda install pandas
1
conda install matplotlib
1
conda install scikit-learn

在下载过程中建议挂上梯子，若是还不知道怎么挂代理（梯子），请参照文章：计算机基础常识 | 代理，或者，在anaconda配置别的下载源，这里也不多做赘述。建议直接挂代理，更加稳定方便，在很多地方都用的到。

  • 配置Jupyter

是一个功能强大的交互式计算平台，它将代码、文档和可视化结果结合在一起，非常适合数据分析、机器学习和教学等场景。通过 Jupyter，用户可以轻松地进行实验、记录和分享分析过程，极大地提高了工作效率和可读性。

这里建议直接在VS_Code中配置，这样会在使用Jupyter的时候方便很多，例如，不需要每次都输入命令行来打开文件，可以享受VS_Code的多种插件比如ai，UI也会美观很多，而且与Anaconda环境的使用也很兼容。

在VS_Code中下载Jupyter插件包。

image

使用也很简单，在VS_Code中，打开命令面板 （Ctrl+Shift+P）并输入Jupyter: Create New Jupyter Notebook ，选择创建笔记本文件 。

image

随后点击选择内核来选择您的内核，这里选择你创建好的Anaconda环境，然后开始编码！

image

代码实践

任务： 基于数据，建立线性回归模型，预测x = 3.5对应的函数值，评估模型的表现。

In [21]:

1
2
3
4
# 加载数据
import pandas as pd
data = pd.read_csv('test.csv')
data.head()

Out[21]:

x y
0 1 7
1 2 9
2 3 11
3 4 13
4 5 15

In [22]:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
# 处理数据
x = data.loc[:,'x']
y = data.loc[:,'y']
print(x,y)
0     1
1     2
2     3
3     4
4     5
5     6
6     7
7     8
8     9
9    10
Name: x, dtype: int64 0     7
1     9
2    11
3    13
4    15
5    17
6    19
7    21
8    23
9    25
Name: y, dtype: int64

In [23]:

1
2
3
4
5
# 展示图形
import matplotlib.pyplot as plt 
plt.figure() #创建一个空白窗口
plt.scatter(x, y) #创建散点图
plt.show() #展示图形

No description has been provided for this image

In [24]:

1
2
3
# 建立模型
from sklearn.linear_model import LinearRegression
model = LinearRegression() #创建线性回归模型

In [25]:

1
2
3
4
# 处理数据（转换维度）
import numpy as np
x = np.array(x).reshape(-1, 1) #将x转换为二维数组
y = np.array(y).reshape(-1, 1) #将y转换为二维数组

In [26]:

1
lr = model.fit(x, y) #训练模型

In [27]:

1
2
3
4
5
6
7
8
9
10
11
12
13
# 预测
y_predict = model.predict(x) #预测
print(y_predict) #打印预测结果
[[ 7.]
 [ 9.]
 [11.]
 [13.]
 [15.]
 [17.]
 [19.]
 [21.]
 [23.]
 [25.]]

In [28]:

1
2
3
Y = lr.predict([[3.5]]) #预测
print(Y) #打印预测结果
[[12.]]

In [29]:

1
2
3
4
5
# a/b 打印
a = lr.coef_ #获取斜率
b = lr.intercept_ #获取截距
print(a,b)
[[2.]] [5.]

In [30]:

1
2
3
4
5
6
# 模型评估
from sklearn.metrics import mean_squared_error, r2_score
r2 = r2_score(y, y_predict) #决定系数
mse = mean_squared_error(y, y_predict) #均方误差
print(mse,r2) 
1.4909471108677122e-29 1.0

In [31]:

1
2
3
4
# 通过图像对比
plt.figure() #创建一个空白窗口
plt.plot(y,y_predict) #创建图
plt.show() #展示图形

No description has been provided for this image

  • 均方误差 (Mean Squared Error, MSE)

    • 定义: MSE 衡量的是预测值与真实值之间差的平方的均值。

    • $$
      MSE = \frac{1}{n} \sum_{i=1}^{n} (y_i - \hat{y}_i)^2
      $$

    • n 是样本数量。

    • yi 是第 i 个样本的真实值。

    • y^i 是第 i 个样本的预测值。

  • 决定系数 (R-squared, r^2)

  • 定义: R2 衡量的是模型对因变量（目标变量）方差的解释程度。它表示因变量中可以由自变量（特征）预测的变异性比例。

  • $$
    R^2 = 1 - \frac{\sum_{i=1}^{n} (y_i - \hat{y}i)^2}{\sum{i=1}^{n} (y_i - \bar{y})^2} = 1 - \frac{SSE}{SST}
    $$

  • yi 是真实值。

  • y^i 是预测值。

  • yˉ 是真实值的平均值。

mse越小越好，r^2越接近1越好。